Find Slope Easily

The concept of slope is fundamental in mathematics, particularly in algebra and geometry. It represents the measure of how steep a line is and can be used to describe the rate of change between two variables. Understanding slope is crucial for solving problems in various fields, including physics, engineering, and economics. In this article, we will delve into the world of slope, exploring its definition, types, and methods for calculation, as well as providing practical examples and applications.

Slope is a measure of the steepness of a line, which can be positive, negative, or zero. A positive slope indicates that the line slopes upward from left to right, while a negative slope means it slopes downward. A zero slope represents a horizontal line. The concept of slope is essential in graphing lines and understanding the relationships between variables. It is used to model real-world phenomena, such as the growth of populations, the motion of objects, and the behavior of financial markets.

The importance of slope cannot be overstated. It has numerous applications in various fields, including science, technology, engineering, and mathematics (STEM). For instance, in physics, slope is used to describe the motion of objects, including the velocity and acceleration of particles. In engineering, slope is used to design roads, bridges, and buildings, ensuring that structures are safe and stable. In economics, slope is used to model the behavior of markets, including the supply and demand of goods and services.

What is Slope?

Slope is a measure of the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. It is often denoted by the letter "m" and can be calculated using the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the two points. The slope of a line can be positive, negative, or zero, depending on the direction of the line.

Types of Slope

There are several types of slope, including: * Positive slope: A line with a positive slope slopes upward from left to right. * Negative slope: A line with a negative slope slopes downward from left to right. * Zero slope: A line with a zero slope is horizontal and has no steepness. * Undefined slope: A line with an undefined slope is vertical and has no horizontal change.

How to Find Slope

There are several methods for finding the slope of a line, including: * Using the slope formula: m = (y2 - y1) / (x2 - x1) * Using the graph of the line: By observing the graph of the line, we can determine the slope by identifying the rise and run between two points. * Using the equation of the line: If we know the equation of the line in slope-intercept form (y = mx + b), we can easily identify the slope (m).

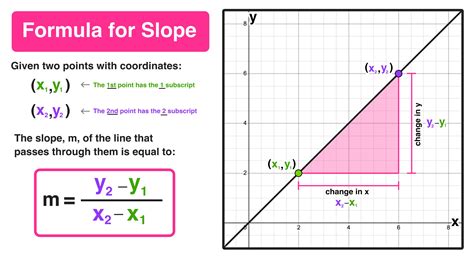
Methods for Finding Slope

Here are some step-by-step methods for finding the slope of a line: 1. Identify the coordinates of two points on the line. 2. Use the slope formula to calculate the slope. 3. Graph the line and identify the rise and run between two points. 4. Use the equation of the line in slope-intercept form to identify the slope.

Applications of Slope

Slope has numerous applications in various fields, including: * Physics: Slope is used to describe the motion of objects, including the velocity and acceleration of particles. * Engineering: Slope is used to design roads, bridges, and buildings, ensuring that structures are safe and stable. * Economics: Slope is used to model the behavior of markets, including the supply and demand of goods and services. * Computer Science: Slope is used in computer graphics to create 3D models and animations.

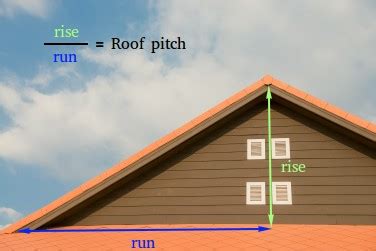
Real-World Examples of Slope

Here are some real-world examples of slope: * The slope of a road: The slope of a road can affect the safety and efficiency of transportation. * The slope of a roof: The slope of a roof can affect the drainage of water and the structural integrity of the building. * The slope of a ski slope: The slope of a ski slope can affect the difficulty and safety of skiing.

Calculating Slope

Calculating slope involves using the slope formula: m = (y2 - y1) / (x2 - x1). This formula can be used to calculate the slope of a line given the coordinates of two points. Alternatively, we can use the graph of the line to identify the rise and run between two points and calculate the slope.

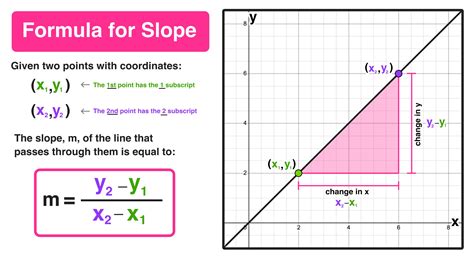
Step-by-Step Slope Calculation

Here are the steps for calculating slope: 1. Identify the coordinates of two points on the line. 2. Plug the coordinates into the slope formula. 3. Calculate the slope using the formula. 4. Simplify the result to get the final answer.

Slope in Graphing

Slope is an essential concept in graphing lines. By understanding the slope of a line, we can graph it accurately and identify its key features, such as the x-intercept and y-intercept. The slope of a line can also be used to determine its equation in slope-intercept form (y = mx + b).

Graphing Lines with Slope

Here are the steps for graphing lines with slope: 1. Identify the slope and y-intercept of the line. 2. Use the slope-intercept form to write the equation of the line. 3. Graph the line using the equation. 4. Identify the x-intercept and y-intercept of the line.

Conclusion and Next Steps

In conclusion, slope is a fundamental concept in mathematics that has numerous applications in various fields. Understanding slope is essential for graphing lines, modeling real-world phenomena, and solving problems in physics, engineering, and economics. By mastering the concept of slope, we can improve our problem-solving skills and develop a deeper understanding of the world around us.

We hope this article has provided you with a comprehensive understanding of slope and its applications. If you have any questions or comments, please feel free to share them below. Additionally, if you're interested in learning more about slope and its applications, we recommend exploring online resources, such as video tutorials and practice problems.

What is the formula for calculating slope?

The formula for calculating slope is m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of two points on the line.

What are the different types of slope?

There are several types of slope, including positive slope, negative slope, zero slope, and undefined slope.

How is slope used in real-world applications?

Slope is used in various fields, including physics, engineering, economics, and computer science, to model real-world phenomena and solve problems.