Intro
Discover the normal AIC value range and its significance in statistical modeling, including Akaike information criterion interpretation, model selection, and evaluation, to improve predictive accuracy and reliability.
The Akaike information criterion, or AIC, is a statistical tool used to evaluate and compare the quality of different models. It was developed by Hirotsugu Akaike in the 1970s and has since become a widely used method for model selection. The AIC value is a relative measure that can be used to determine which model is the most appropriate for a given dataset. In general, the model with the lowest AIC value is considered to be the best model.
Understanding the AIC value range is crucial in determining the quality of a model. The AIC value is calculated based on the log-likelihood function of the model, which is a measure of how well the model fits the data. The AIC value is then adjusted for the number of parameters in the model, which helps to prevent overfitting. Overfitting occurs when a model is too complex and fits the noise in the data rather than the underlying patterns.
A lower AIC value indicates that the model is a better fit for the data, while a higher AIC value indicates that the model is a poorer fit. The AIC value range can vary depending on the specific dataset and models being compared. However, in general, an AIC value difference of 2 or more is considered to be significant, indicating that one model is substantially better than another.
AIC Value Interpretation
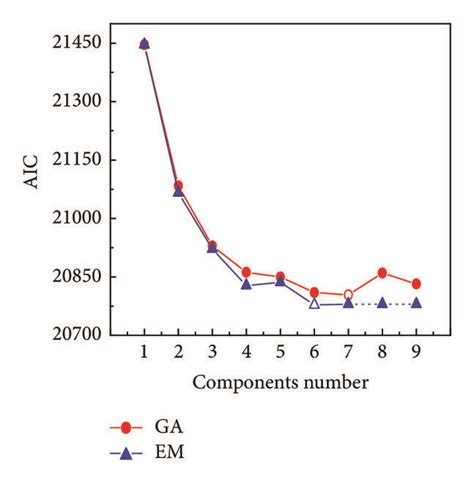
The interpretation of AIC values can be complex, and it is essential to consider the context in which the models are being compared. In general, the AIC value can be interpreted as follows:
- AIC values close to 0 indicate that the model is a good fit for the data.
- AIC values between 0 and 2 indicate that the model is a reasonable fit for the data, but there may be other models that are equally good or better.
- AIC values between 2 and 7 indicate that the model is a moderate fit for the data, and there may be other models that are substantially better.
- AIC values greater than 7 indicate that the model is a poor fit for the data, and other models should be considered.
AIC Value Range for Model Comparison
When comparing multiple models, the AIC value range can be used to determine which model is the most appropriate. The model with the lowest AIC value is considered to be the best model. However, it is essential to consider the context in which the models are being compared and to evaluate the AIC value in conjunction with other metrics, such as the Bayesian information criterion (BIC) and the coefficient of determination (R-squared).Model Selection Using AIC
Model selection using AIC involves comparing the AIC values of different models and selecting the model with the lowest AIC value. This approach can be used to select the best model from a set of candidate models. The AIC value can be calculated using the following formula: AIC = 2k - 2ln(L), where k is the number of parameters in the model, and L is the likelihood function of the model.
The AIC value can be used to compare models with different numbers of parameters, which helps to prevent overfitting. Overfitting occurs when a model is too complex and fits the noise in the data rather than the underlying patterns. By using the AIC value to compare models, researchers can select the model that best balances model complexity and fit to the data.
Advantages of Using AIC for Model Selection
There are several advantages to using AIC for model selection: - AIC is a widely used and well-established method for model selection. - AIC can be used to compare models with different numbers of parameters, which helps to prevent overfitting. - AIC is relatively easy to calculate and interpret. - AIC can be used to select the best model from a set of candidate models.Common Applications of AIC

AIC has a wide range of applications in statistics and data analysis. Some common applications of AIC include:
- Model selection: AIC can be used to select the best model from a set of candidate models.
- Regression analysis: AIC can be used to evaluate the quality of different regression models.
- Time series analysis: AIC can be used to evaluate the quality of different time series models.
- Machine learning: AIC can be used to evaluate the quality of different machine learning models.
Limitations of AIC
While AIC is a widely used and well-established method for model selection, it has several limitations: - AIC is a relative measure, and it can only be used to compare models that are nested within each other. - AIC is sensitive to the choice of model parameters, and it can be influenced by the choice of prior distributions. - AIC can be difficult to interpret, especially for complex models.Alternatives to AIC

There are several alternatives to AIC, including:
- Bayesian information criterion (BIC): BIC is a Bayesian alternative to AIC that uses a different prior distribution.
- Cross-validation: Cross-validation is a method for evaluating the quality of a model by splitting the data into training and testing sets.
- Bootstrap sampling: Bootstrap sampling is a method for evaluating the quality of a model by resampling the data with replacement.
Best Practices for Using AIC
There are several best practices for using AIC: - Use AIC in conjunction with other metrics, such as BIC and R-squared. - Evaluate the AIC value in the context of the research question and the data. - Use AIC to compare models that are nested within each other. - Avoid using AIC to compare models that are not nested within each other.Real-World Examples of AIC

AIC has a wide range of real-world applications. Some examples include:
- Evaluating the quality of different models for predicting stock prices.
- Selecting the best model for predicting customer churn.
- Evaluating the quality of different models for predicting disease risk.
- Selecting the best model for predicting energy consumption.
Future Directions for AIC
There are several future directions for AIC, including: - Developing new methods for calculating AIC that are more efficient and accurate. - Developing new methods for interpreting AIC that are more intuitive and easy to understand. - Applying AIC to new areas, such as machine learning and deep learning. - Developing new alternatives to AIC that are more robust and reliable.What is the Akaike information criterion (AIC)?
+The Akaike information criterion (AIC) is a statistical tool used to evaluate and compare the quality of different models.
How is the AIC value calculated?
+The AIC value is calculated using the formula: AIC = 2k - 2ln(L), where k is the number of parameters in the model, and L is the likelihood function of the model.
What is the difference between AIC and BIC?
+AIC and BIC are both used for model selection, but they use different prior distributions. AIC is a more general method, while BIC is a Bayesian alternative.
Can AIC be used for non-nested models?
+No, AIC can only be used to compare models that are nested within each other.
What are the limitations of AIC?
+AIC is a relative measure, and it can only be used to compare models that are nested within each other. It is also sensitive to the choice of model parameters and can be influenced by the choice of prior distributions.
We hope this article has provided a comprehensive overview of the Akaike information criterion (AIC) and its applications in statistics and data analysis. AIC is a powerful tool for model selection, and it has a wide range of applications in fields such as economics, finance, and machine learning. If you have any questions or comments, please feel free to share them below. Additionally, if you found this article helpful, please consider sharing it with your colleagues and friends.
