5 Ways To Find Er

The world of mathematics is full of intriguing concepts, and one of the most fascinating is the idea of finding the value of "e," a fundamental constant in mathematics approximately equal to 2.71828. This constant is crucial in various mathematical fields, including calculus, number theory, and finance. The significance of "e" lies in its unique properties and its appearance in numerous mathematical formulas, making it a cornerstone of mathematical analysis.

Understanding "e" and its applications can deepen one's appreciation for the intricacies of mathematics and its pervasive influence on science, technology, and everyday life. From the calculation of compound interest to the modeling of population growth, "e" plays a pivotal role. Its importance extends beyond the realm of mathematics, impacting fields such as economics, biology, and engineering.

The discovery and calculation of "e" have been gradual, with contributions from many mathematicians over the centuries. The earliest hints of "e" can be traced back to the works of John Napier and Jacob Bernoulli, but it was Leonhard Euler who first introduced the notation and explored its properties extensively. Today, "e" is recognized as a fundamental element in mathematical expressions, especially in those involving exponential growth or decay.

Introduction to the Value of e

The value of "e" is approximately 2.71828, but it is an irrational number, meaning it cannot be expressed as a finite decimal or fraction. This property makes "e" fascinating and challenging to study. Its irrationality implies that "e" has an infinite number of digits, and these digits never repeat in a predictable pattern. The calculation of "e" to a high degree of precision has been a subject of interest for mathematicians and computer scientists, with advancements in computational power enabling the calculation of "e" to millions of digits.

Historical Background of e

The history of "e" is intertwined with the development of calculus and the study of exponential functions. The first hints of "e" emerged in the 17th century, but it wasn't until the 18th century, with the work of Euler, that "e" was fully recognized and explored. Euler's work not only introduced the notation "e" but also demonstrated its significance in various mathematical contexts, including calculus and number theory. Since then, "e" has become a cornerstone of mathematical education and research, appearing in countless formulas and theorems.

Mathematical Definition of e

Mathematically, "e" is defined as the base of the natural logarithm, which is the inverse function of the natural exponential function. One of the most famous and elegant definitions of "e" is through the infinite series: \[ e = \sum_{n=0}^{\infty} \frac{1}{n!} = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots \] This series converges to "e," illustrating the fundamental connection between "e" and the factorial function. Another definition, which is closely related to the concept of continuous compounding, is given by the limit: \[ e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n \] This limit shows how "e" arises naturally in the context of exponential growth and compound interest.

Applications of e in Mathematics

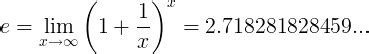
The applications of "e" in mathematics are vast and varied. In calculus, "e" is crucial for understanding exponential growth and decay, which models a wide range of phenomena, from population dynamics to chemical reactions. The derivative of the exponential function \(f(x) = e^x\) is \(f'(x) = e^x\), showing that the rate of change of the exponential function is the function itself, a unique property that underscores the importance of "e" in differential equations.

In probability theory, "e" appears in the description of the normal distribution and the Poisson distribution, highlighting its role in statistical analysis and modeling. Furthermore, "e" is essential in finance, particularly in the calculation of compound interest, where it represents the idea of continuous compounding. The formula for continuous compounding, (A = Pe^{rt}), where (A) is the amount after (t) years, (P) is the principal amount, (r) is the annual interest rate, and (t) is the time the money is invested for, demonstrates how "e" is used to model financial growth.

Calculating e

Calculating "e" to a high degree of precision has been a challenge that has intrigued mathematicians and computer scientists for centuries. Several methods exist, ranging from the use of infinite series to more complex algorithms that rely on mathematical properties of "e." One of the simplest methods to calculate "e" is through the use of the series: \[ e = \sum_{n=0}^{\infty} \frac{1}{n!} \] However, for high precision, more sophisticated methods are required, such as the Gauss-Legendre algorithm or the use of arithmetic-geometric mean.

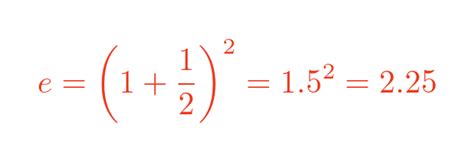
Methods for Calculating e

Several methods can be employed to calculate "e," each with its advantages and limitations: - **Infinite Series:** The most straightforward method, using the series \(e = \sum_{n=0}^{\infty} \frac{1}{n!}\). - **Limit Definition:** Using the limit \(e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n\). - **Gauss-Legendre Algorithm:** A fast method for computing "e" to a high degree of precision, based on the arithmetic-geometric mean of two numbers. - **Computational Software:** Utilizing computer software that can handle high-precision arithmetic to calculate "e" to millions of digits.

Conclusion and Future Directions

In conclusion, "e" is a fascinating mathematical constant with profound implications across various fields. Its unique properties and appearances in numerous mathematical formulas make it a cornerstone of mathematical analysis. The calculation of "e" to a high degree of precision continues to be an area of interest, with advancements in computational power enabling new records in the number of digits calculated.

As mathematics continues to evolve, the study of "e" and its applications will remain a vibrant area of research, with potential impacts on our understanding of exponential growth, calculus, and probability theory. For those interested in exploring "e" further, there are numerous resources available, from mathematical texts to computational software, inviting a deeper dive into the mysteries and applications of this fundamental constant.

What is the approximate value of e?

+

The approximate value of e is 2.71828.

Why is e considered a fundamental constant in mathematics?

+

e is considered fundamental because it appears in numerous mathematical formulas, particularly in those involving exponential growth or decay, and has unique properties that make it essential for calculus and other areas of mathematics.

How is e calculated to a high degree of precision?

+

e can be calculated using various methods, including infinite series, limit definitions, and sophisticated algorithms like the Gauss-Legendre algorithm, which allow for the calculation of e to millions of digits with the aid of computational software.

We hope this comprehensive overview of "e" has sparked your interest in this fascinating mathematical constant. Whether you're a seasoned mathematician or just beginning to explore the world of mathematics, "e" offers a wealth of knowledge and application that can deepen your understanding and appreciation of mathematical concepts. Feel free to share your thoughts, ask questions, or explore further the intriguing world of mathematics and its constants.